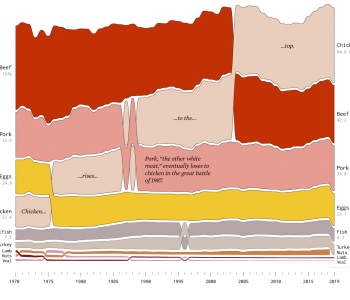
 Data
Data
Nassim Taleb calls Nate Silver totally clueless about probability:…
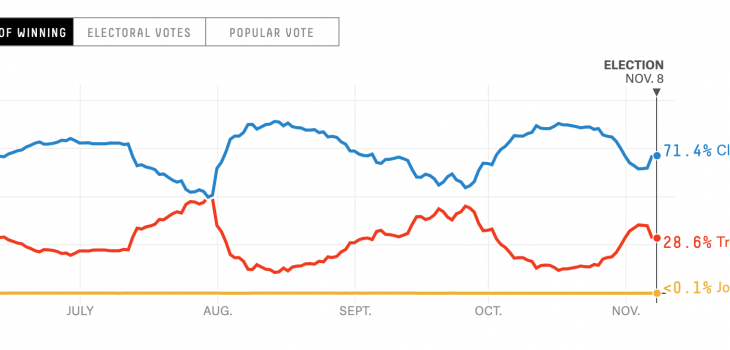
Good summation of the onoing Nate Silver/Nassim Taleb battle in this article. However, the main point is an important one applicable more broadly than elections when talking about predictions: certainty. The problem and valid criticism with Silver’s forecasts is that there is no certainty given with them. A margin of error is not a replacement for that. That, coupled with daily changes that, at times, can be dramatic when looked at on a broader time series, makes it misleading.
Whenever you or someone around you is forecasting something, ask for their prediction and what their level of certainty is. For example, if you’re a product manager with a B2B sales team and one of the sales people is trying to influence your product plan by telling you they could land a $10m account if you added this one, otherwise obscure, feature, ask them their level of certainty. If its 80%+, then it probably should be high on the list based on their ROI analysis. If its 50% or lower, maybe not. And make sure they know their name is going to be next to that certainty %.
To paraphrase Taleb, if I tell you an event has a 0% chance of occurring, I cannot change my mind and tell you tomorrow it now has a 50% chance of occurring. Otherwise I shouldn’t have told you it has a 0% chance in the first place. Probability and confidence are inextricably linked, and the number a pollster predicts should encapsulate both. To go to the other extreme, if the uncertainty is extremely high (and therefore confidence low), it does not matter what the polls today are saying. I should give both candidates a 50% chance of winning, because I am admitting the extremely likely possibility that an external event will happen that will invalidate today’s polls. To put it in technical terms, maximum uncertainty implies maximum entropy, and the maximum entropy distribution on the [0, 1] interval is the uniform distribution, which has a mean at .5. The following figure (from this paper) shows the relationship between probability (x-axis) and volatility (y-axis) under a specific option pricing formulation.
http://quant.am/statistics/2020/10/11/taleb-silver-feud/